谨以此篇献给学无止境的自己-----------silence-breaker
初步认识矩阵
从线性方程组入手
生活中我们常常需要通过求方程组的解来解决一些数学问题,对于一些比较特殊的方程组,如线性方程组:
0 x 1 − 1 y 1 = x 2 − 2 x 1 + 0 y 1 = y 2 \begin{aligned}
0x_{1}-1y_{1}=x_{2}\\
-2x_{1}+0y_{1}=y_{2} \\
\end{aligned} 0 x 1 − 1 y 1 = x 2 − 2 x 1 + 0 y 1 = y 2 我们可以把它们写成一种简约的形式:
( 0 − 1 − 2 0 ) ( x 1 y 1 ) = ( x 2 y 2 ) \begin{pmatrix}
0&-1 \\
-2&0 \\
\end{pmatrix}
\begin{pmatrix}
x_{1} \\
y_{1} \\
\end{pmatrix}
=\begin{pmatrix}
x_{2} \\
y_{2} \\
\end{pmatrix} ( 0 − 2 − 1 0 ) ( x 1 y 1 ) = ( x 2 y 2 ) 这是从线性方程组入手写出来的矩阵方程
从向量方程入手
如何理解一个矩阵
首先我们来熟悉一些概念,我们怎么表达向量,向量之间是如何进行转换计算的,向量之间的关系是什么,什么是向量空间…
初高中我们就已经开始接触向量,不过那时候我们通常用的是 ( 1 , 2 ) (1,2) ( 1 , 2 )
( 1 , 2 ) → ( 1 2 ) (1,2)\to \begin{pmatrix}
1 \\
2
\end{pmatrix} ( 1 , 2 ) → ( 1 2 ) 可以看到右边括号中,一行代表一个维度,一列代表一个向量(至于为什么这么写,是为了之后方便理解和计算),像这样只有一列的向量我们称之为列向量
那么如何表达一个空间中的一组基呢?显然,我们把不同的列向量拼在一起
( 1 0 0 1 ) \begin{pmatrix}
1&0 \\
0&1
\end{pmatrix} ( 1 0 0 1 ) 这个就是二维空间中最经典的标准基,我们定义左边的为向量 i ⃗ \vec{i} i j ⃗ \vec{j} j
( 1 0 0 1 ) → ( 0 − 1 2 0 ) \begin{pmatrix}
1&0 \\
0&1
\end{pmatrix}\to \begin{pmatrix}
0&-1 \\
2&0
\end{pmatrix} ( 1 0 0 1 ) → ( 0 2 − 1 0 ) 这个变换过程就是将这组基逆时针旋转 90°,然后第一个向量拉长为原来的两倍。更进一步的,可以把这个过程想象成直角坐标系(空间被划分为无数个等大的小方格)连带着向量伸缩,旋转的过程。值得注意的是,在这种变换过程中,无论我们怎么伸缩、旋转,我们的原点始终不会变,空间仍然被分为很多个相同的小方格(保持网格线平行且等距分布),这种变换我们称之为线性变换 (几何层面感性的理解)
线性变换 ,我们常常定义 T ( x ⃗ ) T(\vec{x}) T ( x ) T T T x ⃗ \vec{x} x
T ( x ⃗ + y ⃗ ) = T ( x ⃗ ) + T ( y ⃗ ) T ( c ⃗ x ) = c T ( x ⃗ ) \begin{aligned}
T(\vec{x}+\vec{y})=T(\vec{x})+T(\vec{y})
\\T(\vec{c}x)=cT(\vec{x})
\end{aligned} T ( x + y ) = T ( x ) + T ( y ) T ( c x ) = c T ( x ) 通常我们通过对一个向量做线性变换,然后得到另一个向量,即:
T ( x ⃗ ) = b ⃗ T(\vec{x})=\vec{b} T ( x ) = b 这是一个很抽象的表达式,继续拿刚刚旋转 90°,i ⃗ \vec{i} i b ⃗ \vec{b} b d ⃗ \vec{d} d b ⃗ \vec{b} b i ⃗ , j ⃗ \vec{i},\vec{j} i , j b ⃗ \vec{b} b
( 0 − 1 2 0 ) ( x 1 y 1 ) = ( x 2 y 2 ) → ( 0 2 ) x 1 + ( − 1 0 ) y 1 = ( x 2 y 2 ) \begin{pmatrix}
0&-1 \\
2&0
\end{pmatrix}\begin{pmatrix}
x_{1} \\
y_{1}
\end{pmatrix}=\begin{pmatrix}
x_{2} \\
y_{2}
\end{pmatrix}
\to \begin{pmatrix}
0 \\
2
\end{pmatrix}x_{1}+\begin{pmatrix}
-1 \\
0
\end{pmatrix}y_{1}=\begin{pmatrix}
x_{2} \\
y_{2}
\end{pmatrix} ( 0 2 − 1 0 ) ( x 1 y 1 ) = ( x 2 y 2 ) → ( 0 2 ) x 1 + ( − 1 0 ) y 1 = ( x 2 y 2 ) 这样,是不是就可以和最开始的线性方程组联系起来了?因此矩阵(向量)方程最终都可以转化为线性方程组的形式
我们再进一步对矩阵进行理解,形如
( 1 2 3 4 5 6 ) \begin{pmatrix}
1&2&3 \\
4&5&6
\end{pmatrix} ( 1 4 2 5 3 6 ) 可以看作三维向量向二维空间的转换(列数是原来空间的向量的个数,写出来的数字是每一个向量变换后的结果)
( a 0 0 0 a 0 0 0 a ) \begin{pmatrix}
a&0&0 \\
0&a&0 \\
0&0&a
\end{pmatrix} a 0 0 0 a 0 0 0 a 可以看作三维每个坐标轴伸长为原来的 a 倍,如果 a 为 1 那么就相当于对原来的坐标系不做任何变换,这种矩阵叫做单位阵
一般性矩阵乘法
那么对于一般的矩阵方程我们应该如何运算呢?
从上面的例子中我们得知,代表线性变换的矩阵的列数(左侧)必须与进行变换的矩阵行数(右侧)相等,本质上来说就是进行变换的维度一一对应 (R m ∗ n ∗ R n ∗ q = R m ∗ q R^{m*n}*R^{n*q}=R^{m*q} R m ∗ n ∗ R n ∗ q = R m ∗ q
( a 11 a 12 … a 1 n . . a m 1 a m 2 … a m n ) ( b 11 b 12 … b 1 q . . b n 1 a n 2 … a n q ) \begin{pmatrix}
a_{11}&a_{12}&\dots a_{1n} \\
. \\
. \\
a_{m1}&a_{m2}&\dots a_{mn}
\end{pmatrix}\begin{pmatrix}
b_{11}&b_{12}&\dots b_{1q} \\
. \\
. \\
b_{n1}&a_{n2}&\dots a_{nq}
\end{pmatrix} a 11 . . a m 1 a 12 a m 2 … a 1 n … a mn b 11 . . b n 1 b 12 a n 2 … b 1 q … a n q 这似乎一下子看会有点懵,若以矩阵分块 思想,可以很好的和刚刚的例子联系起来
矩阵分块 形象地来说就是把矩阵当作蛋糕一样横着切竖着切,形成一个个子矩阵
( a 11 a 12 … a 1 n . . a m 1 a m 2 … a m n ) ( b 1 b 2 . b n ) = ( a 11 . . a m 1 ) b 1 + ⋯ + ( a 1 n . . a m n ) b n = ( a 11 b 1 + … a 1 n b n . . a m 1 b 1 + … a m n b n ) = ( ∑ k = 1 n a 1 k b k q ⋯ ∑ k = 1 n a 1 k b k q . . ∑ k = 1 n a m k b k 1 ⋯ ∑ k = 1 n a m k b k q ) \begin{aligned}
\begin{pmatrix}
a_{11}&a_{12}&\dots a_{1n} \\
. \\
. \\
a_{m1}&a_{m2}&\dots a_{mn}
\end{pmatrix}\begin{pmatrix}
b_{1} \\
b_{2} \\
. \\
bn
\end{pmatrix}
\\=\begin{pmatrix}
a_{11} \\
. \\
. \\
a_{m1}
\end{pmatrix}b_{1}+\dots+\begin{pmatrix}
a_{1n} \\
. \\
. \\
a_{mn}
\end{pmatrix}b_{n}
\\=\begin{pmatrix}
a_{11}b_{1}+\dots a_{1n}b_{n} \\
. \\
. \\
a_{m1}b_{1}+\dots a_{mn}b_{n}
\end{pmatrix}
\\=\begin{pmatrix}
\sum_{k=1}^{n}a_{1k}b_{k_q}& \dots \sum_{k=1}^{n}a_{1k}b_{kq} \\
. \\
. \\
\sum_{k=1}^{n}a_{mk}b_{k1}& \dots \sum_{k=1}^{n}a_{mk}b_{kq}
\end{pmatrix}
\end{aligned} a 11 . . a m 1 a 12 a m 2 … a 1 n … a mn b 1 b 2 . bn = a 11 . . a m 1 b 1 + ⋯ + a 1 n . . a mn b n = a 11 b 1 + … a 1 n b n . . a m 1 b 1 + … a mn b n = ∑ k = 1 n a 1 k b k q . . ∑ k = 1 n a mk b k 1 ⋯ ∑ k = 1 n a 1 k b k q ⋯ ∑ k = 1 n a mk b k q 所以我们可以得到矩阵解的 c i j = ∑ k = 1 n a i k b k j c_{ij}=\sum_{k=1}^{n}a_{ik}b_{kj} c ij = ∑ k = 1 n a ik b kj
A B ≠ B A AB\neq BA A B = B A 初等行变换
矩阵的初等操作包括 interchange(行交换), scaling(行倍增), replacement(c r i + r j → r j cr_{i}+r_{j}\to r_{j} c r i + r j → r j
行列式
大多数人在学习线性代数的时候都知道如何计算行列式,但对于它本身的意义却并不清晰
其实从几何的角度理解,行列式代表了变换后面积与变换前面积的比例 (这个理解对于后续行列式相关性质的理解至关重要)
首先我们从二维空间开始
A = ( 1 0 0 1 ) → B = ( 2 0 0 2 ) ∣ A ∣ = 1 , ∣ B ∣ = 4 \begin{aligned}
A=\begin{pmatrix}
1&0 \\
0&1
\end{pmatrix}\to B=\begin{pmatrix}
2&0 \\
0&2
\end{pmatrix}
\\[0.5cm]
|A|=1,|B|=4
\end{aligned} A = ( 1 0 0 1 ) → B = ( 2 0 0 2 ) ∣ A ∣ = 1 , ∣ B ∣ = 4 A 的行列式看作两个向量所围成的 1* 1 方块面积,B 的行列式看作 2* 2 方块面积,相当于由 A 变成 B,向量所围面积是原来的 4 倍
接下来做更一般性推广
A ′ = ( a b c d ) ∣ A ∣ = a d − b c \begin{aligned}
A'=\begin{pmatrix}
a&b \\
c&d
\end{pmatrix}
\\[0.5cm]
|A|=ad-bc
\end{aligned} A ′ = ( a c b d ) ∣ A ∣ = a d − b c 按我们的猜想,从 A 变换成 A‘,面积扩大为原来的 a d − b c ad-bc a d − b c
a 和 d 分别为原来两个基向量方向扩大的倍数,所以如果 b c 为 0,那么 a d 显然就是面积扩大的倍数
若 c 不等于零,b 等于 0,也就是说,x 方向向量不仅延长为原来 a 倍后还向上移动了 c 个单位,这相当于把第一种情况扩大的矩形搓成了一个平行四边形,面积不变
若 a b c d 都不等于 0,如果说 a d 表示在水平竖直方向上的拉伸压缩,那么 b c 体现的就是平行四边形在对角方向上的拉伸压缩(这应该很容易想象)下图是严格的推导
∣ n ∗ c o l 1 m ∗ c o l 2 … c o l n ∣ = n m ∣ c o l 1 c o l 2 … c o l n ∣ ∣ c o l 1 c o l 2 … c o l n ∣ = − ∣ c o l 2 c o l 1 … c o l n ∣ ∣ c o l 1 c ∗ c o l 1 + c o l 2 c o l 3 … c o l n ∣ = ∣ c o l 1 c o l 2 c o l 3 … c o l n ∣ ∣ A B ∣ = ∣ A ∣ ∣ B ∣ \begin{aligned}
\begin{vmatrix}
n*col_{1}&m*col_{2}&\dots&col_{n}
\end{vmatrix}=nm\begin{vmatrix}
col_{1}&col_{2}&\dots&col_{n}
\end{vmatrix}
\\\begin{vmatrix}
col_{1}&col_{2}&\dots&col_{n}
\end{vmatrix}=-\begin{vmatrix}
col_{2}&col_{1}&\dots&col_{n}
\end{vmatrix}\\
\begin{vmatrix}
col_{1}&c*col_{1}+col_{2}&col_{3}\dots col_{n}
\end{vmatrix}=\begin{vmatrix}
col_{1}&col_{2}&col_{3} \dots col_{n}
\end{vmatrix}
\\\begin{vmatrix}
AB
\end{vmatrix}=\begin{vmatrix}
A
\end{vmatrix}\begin{vmatrix}
B
\end{vmatrix}
\end{aligned} n ∗ co l 1 m ∗ co l 2 … co l n = nm co l 1 co l 2 … co l n co l 1 co l 2 … co l n = − co l 2 co l 1 … co l n co l 1 c ∗ co l 1 + co l 2 co l 3 … co l n = co l 1 co l 2 co l 3 … co l n A B = A B (对第二条做进一步解释)列互换相当于从右手系变成左手系,行列式*(-1),再互换一次,相当于从左手系变成右手系,行列式*(-1)
(对第三条做进一步解释)c o l 2 col_{2} co l 2 n ∗ c o l 1 n*col_{1} n ∗ co l 1 第四条性质 :
∣ c o l 1 c o l 2 + c o l ′ … c o l n ∣ = ∣ c o l 1 c o l 2 … c o l n ∣ + ∣ c o l 1 c o l ′ … c o l n ∣ \begin{aligned}
\begin{vmatrix}
col_{1}&col_{2}+col'&\dots&col_{n}
\end{vmatrix}=\begin{vmatrix}
col_{1}&col_{2}&\dots&col_{n}
\end{vmatrix}+\begin{vmatrix}
col_{1}&col'&\dots&col_{n}
\end{vmatrix}
\end{aligned} co l 1 co l 2 + co l ′ … co l n = co l 1 co l 2 … co l n + co l 1 co l ′ … co l n 或许有人对行列式的行操作存在疑惑(因为上面都以列操作为例),你只需要设定一组新的规则,每行表示一个向量,每列表示一个维度即可
关于主对角线和副对角线行列式计算结论 :
易得如果元素全部位于主对角线,就相当于在右手系下每一个维度乘上一个常数,副对角线可以通过行变换成主对角线去计算。
如果行列式成主倒三角型(即 echelon 阶梯型)(元素都在主对角线及之上),这也很好理解:先写上主对角线的数字,从最左边依次做 replacement 填充主对角线上面的数字,这时候做变换并不影响行列式的大小,所以 echelon 阶梯型行列式的大小就是主对角线上数字的乘积
高阶行列式(如何理解余子式)
对于二阶以上的行列式我们采用以下公式计算
首先引入代数余子式 概念:A i j = ( − 1 ) i + j ∣ A i j ∣ ‾ A_{ij}=(-1)^{i+j}|\overline{A_{ij}|} A ij = ( − 1 ) i + j ∣ A ij ∣ 余子式的含义 ,我们拿一个具体的例子来说:
A = ( 1 2 3 4 5 6 7 8 9 ) A=\begin{pmatrix}
1&2&3 \\
4&5&6 \\
7&8&9
\end{pmatrix} A = 1 4 7 2 5 8 3 6 9 ∣ A ∣ |A| ∣ A ∣
∣ 5 6 8 9 ∣ ∣ 4 6 7 9 ∣ ∣ 4 5 7 8 ∣ \begin{vmatrix}
5&6 \\
8&9
\end{vmatrix}\,\begin{vmatrix}
4&6 \\
7&9
\end{vmatrix}\,\begin{vmatrix}
4&5 \\
7&8
\end{vmatrix} 5 8 6 9 4 7 6 9 4 7 5 8 我们思考一下得到余子式的过程,我们去掉第一行,相当于把 x 轴砍掉,变成了 y, z 轴围成的二维平面,而余子式表示的就是 y o z yoz yoz
而求 ∣ A ∣ |A| ∣ A ∣ y o z yoz yoz
求解方程
矩阵的逆
在上一章我们探讨了矩阵对应的线性变换,了解了正向的矩阵乘法。在实际应用中,我们通常用于求解方程的解,这是一个逆向的过程
A x ⃗ = b ⃗ x ⃗ = A − 1 b ⃗ \begin{aligned}
A\vec{x}=\vec{b}\\
\vec{x}=A^{-1}\vec{b}
\end{aligned} A x = b x = A − 1 b 因此,求出矩阵的逆成为求解方程组的关键。从几何的角度理解,就是将线性变换的操作反过来进行
可以推知,矩阵的逆具有以下性质
A − 1 A = A A − 1 = I ( 单位阵 ) A^{-1}A=AA^{-1}=I(单位阵) A − 1 A = A A − 1 = I ( 单位阵 ) 如何求出矩阵的逆?
法 1: (E 表示对矩阵做的行操作)
A → E 1 A → E 2 E 1 A → ⋯ → E n E n − 1 … E 1 A = I → E n E n − 1 … E 1 = A − 1 ( A I ) → ( E n E n − 1 … E 1 A E n E n − 1 … E 1 I ) → ( I A − 1 ) \begin{aligned}
A\to E_{1}A\to E_{2}E_{1}A\to\dots\to E_{n}E_{n-1}\dots E_{1}A=I\to E_{n}E_{n-1}\dots E_{1}=A^{-1}\\
\begin{pmatrix}
A&I
\end{pmatrix}\to \begin{pmatrix}
E_{n}E_{n-1}\dots E_{1}A&E_{n}E_{n-1}\dots E_{1}I
\end{pmatrix}\to \begin{pmatrix}
I&A^{-1}
\end{pmatrix}
\end{aligned} A → E 1 A → E 2 E 1 A → ⋯ → E n E n − 1 … E 1 A = I → E n E n − 1 … E 1 = A − 1 ( A I ) → ( E n E n − 1 … E 1 A E n E n − 1 … E 1 I ) → ( I A − 1 ) 法 2:
A − 1 = A ∗ ∣ A ∣ A^{-1}=\frac{A^{*}}{|A|} A − 1 = ∣ A ∣ A ∗ 伴随矩阵定义
A ∗ = ( A 11 A 21 … A n 1 . . A 1 n A 2 n … A n n ) A^*=\begin{pmatrix}
A_{11}&A_{21}&\dots&A_{n_{1}} \\
. \\
. \\
A_{1n}&A_{2n}&\dots&A_{nn}
\end{pmatrix} A ∗ = A 11 . . A 1 n A 21 A 2 n … … A n 1 A nn 证明逆矩阵的式子相当于证明:
A A ∗ = ∣ A ∣ I AA^*=|A|I A A ∗ = ∣ A ∣ I (鉴于同济版的书上有证明过程所以这里不再赘述)可以发现结果矩阵中只有对角线上的元素不为零且大小为 ∣ A ∣ |A| ∣ A ∣
矩阵逆的存在性
并不是所有矩阵都存在逆矩阵,当行列式为 0 时逆矩阵不存在,那么如何理解这个点呢?
根据上文,行列式为 0 时意味着矩阵变换降维,例如三维的体积压缩成了一个面,二维的面积压缩成了一个点。如:
( 1 1 0 0 ) \begin{aligned}
\begin{pmatrix}
1&1 \\
0&0
\end{pmatrix}
\end{aligned} ( 1 0 1 0 ) 如果你要还原成原来的标准基形式,你需要把一条线拓展成一个面,无论你怎么旋转,伸长,压缩,始终还是一条线,所以行列式为 0 的时候逆矩阵不存在
克莱姆法则
对于一般的线性方程组:
3 x 1 + 4 x 2 + 5 x 3 = 7 x 1 + 9 x 2 + 7 x 3 = 8 5 x 1 + 7 x 2 + 10 x 3 = 5 \begin{aligned}
3x_{1}+4x_{2}+5x_{3}=7\\
x_{1}+9x_{2}+7x_{3}=8\\
5x_{1}+7x_{2}+10x_{3}=5
\end{aligned} 3 x 1 + 4 x 2 + 5 x 3 = 7 x 1 + 9 x 2 + 7 x 3 = 8 5 x 1 + 7 x 2 + 10 x 3 = 5 我们写成矩阵形式进行求解
( 3 4 5 1 9 7 5 7 10 ) ( x 1 x 2 x 3 ) = ( 7 8 5 ) = b ⃗ \begin{pmatrix}
3&4&5 \\
1&9&7 \\
5&7&10
\end{pmatrix}\begin{pmatrix}
x_{1} \\
x_{2} \\
x_{3}
\end{pmatrix}=\begin{pmatrix}
7 \\
8 \\
5
\end{pmatrix}=\vec{b} 3 1 5 4 9 7 5 7 10 x 1 x 2 x 3 = 7 8 5 = b 按照克莱姆法则我们不需要求矩阵的逆,仅通过计算行列式可以得出每一个解
x 1 = ∣ b ⃗ c o l 2 c o l 3 ∣ ∣ c o l 1 c o l 2 c o l 3 ∣ \begin{aligned}
x_{1}=\frac{\begin{vmatrix}
\vec{b}&col_{2}&col_{3}
\end{vmatrix}}{\begin{vmatrix}
col_{1}&col_{2}&col_{3}
\end{vmatrix}}
\end{aligned} x 1 = co l 1 co l 2 co l 3 b co l 2 co l 3 其余解以此类推,用 b ⃗ \vec{b} b 但是,为什么这么做就可以求出解呢?
为了更形象,这里我们写成(第一个矩阵标记为 A,结果矩阵标记为 B)
( u 1 v 1 w 1 u 2 v 2 w 2 u 3 v 3 w 3 ) ( x y z ) = ( b 1 b 2 b 3 ) \begin{aligned}
\begin{pmatrix}
u_{1}&v_{1}&w_{1} \\
u_{2}&v_{2}&w_{2} \\
u_{3}&v_{3}&w_{3}
\end{pmatrix}\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}=\begin{pmatrix}
b_{1} \\
b_{2} \\
b_{3}
\end{pmatrix}
\end{aligned} u 1 u 2 u 3 v 1 v 2 v 3 w 1 w 2 w 3 x y z = b 1 b 2 b 3 我们可以从体积(行列式)的角度表示 x , y , z x,y,z x , y , z
x = ∣ x 0 0 y 1 0 z 0 1 ∣ y = ∣ 1 x 0 0 y 0 0 z 1 ∣ z = ∣ 1 0 x 0 1 y 0 0 z ∣ \begin{aligned}
x=\begin{vmatrix}
x&0&0 \\
y&1&0 \\
z&0&1
\end{vmatrix}
\\
y=\begin{vmatrix}
1&x&0 \\
0&y&0 \\
0&z&1
\end{vmatrix}
\\
z=\begin{vmatrix}
1&0&x \\
0&1&y \\
0&0&z
\end{vmatrix}
\end{aligned} x = x y z 0 1 0 0 0 1 y = 1 0 0 x y z 0 0 1 z = 1 0 0 0 1 0 x y z 这里很容易想象,体积的大小就是对应某一轴的坐标值
( x y z ) → ( b 1 b 2 b 3 ) ( 0 1 0 ) → ( v 1 v 2 v 3 ) ( 0 0 1 ) → ( w 1 w 2 w 3 ) \begin{aligned}
\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}\to \begin{pmatrix}
b_{1} \\
b_{2} \\
b_{3} \\
\end{pmatrix}
\\
\begin{pmatrix}
0 \\
1 \\
0
\end{pmatrix}\to \begin{pmatrix}
v_{1} \\
v_{2} \\
v_{3}
\end{pmatrix}\\
\begin{pmatrix}
0 \\
0 \\
1
\end{pmatrix}\to \begin{pmatrix}
w_{1} \\
w_{2} \\
w_{3}
\end{pmatrix}
\end{aligned} x y z → b 1 b 2 b 3 0 1 0 → v 1 v 2 v 3 0 0 1 → w 1 w 2 w 3 所以变换后的体积为
∣ x 0 0 y 1 0 z 0 1 ∣ → ∣ b 1 v 1 w 1 b 2 v 2 w 2 b 3 v 3 w 3 ∣ \begin{vmatrix}
x&0&0 \\
y&1&0 \\
z&0&1
\end{vmatrix}\to
\begin{vmatrix}
b_{1}&v_{1}&w_{1} \\
b_{2}&v_{2}&w_{2} \\
b_{3}&v_{3}&w_{3}
\end{vmatrix} x y z 0 1 0 0 0 1 → b 1 b 2 b 3 v 1 v 2 v 3 w 1 w 2 w 3 如果我们知道这两个体积之间的比例是不是就可以把 x 算出来了?
这两个体积之间的比例就是做线性变换操作矩阵的行列式,即:
∣ u 1 v 1 w 1 u 2 v 2 w 2 u 3 v 3 w 3 ∣ ∣ x 0 0 y 1 0 z 0 1 ∣ = ∣ b 1 v 1 w 1 b 2 v 2 w 2 b 3 v 3 w 3 ∣ \begin{vmatrix}
u_{1}&v_{1}&w_{1} \\
u_{2}&v_{2}&w_{2} \\
u_{3}&v_{3}&w_{3}
\end{vmatrix}\begin{vmatrix}
x&0&0 \\
y&1&0 \\
z&0&1
\end{vmatrix}=\begin{vmatrix}
b_{1}&v_{1}&w_{1} \\
b_{2}&v_{2}&w_{2} \\
b_{3}&v_{3}&w_{3}
\end{vmatrix} u 1 u 2 u 3 v 1 v 2 v 3 w 1 w 2 w 3 x y z 0 1 0 0 0 1 = b 1 b 2 b 3 v 1 v 2 v 3 w 1 w 2 w 3 所以我们得到
x = ∣ b 1 v 1 w 1 b 2 v 2 w 2 b 3 v 3 w 3 ∣ ∣ u 1 v 1 w 1 u 2 v 2 w 2 u 3 v 3 w 3 ∣ x=\frac{\begin{vmatrix}
b_{1}&v_{1}&w_{1} \\
b_{2}&v_{2}&w_{2} \\
b_{3}&v_{3}&w_{3}
\end{vmatrix}}{\begin{vmatrix}
u_{1}&v_{1}&w_{1} \\
u_{2}&v_{2}&w_{2} \\
u_{3}&v_{3}&w_{3}
\end{vmatrix}} x = u 1 u 2 u 3 v 1 v 2 v 3 w 1 w 2 w 3 b 1 b 2 b 3 v 1 v 2 v 3 w 1 w 2 w 3 这,就是克莱姆法则的几何理解
高斯消元法
我们在求解方程的时候可以把线性变换矩阵通过多次初等行变换变成主对角线阶梯型(echelon form) ,这样方便计算。这种算法就叫做高斯消元法。值得注意的是,进行初等行变换的时候遵循从左到右,从上到下 的基本原则,把每行第一个不为 0 的数称作 leading entry(先导元素) ,leading entry 所在的列叫做 pivot column(主元列)
( u 1 v 1 w 1 0 v 2 w 2 0 0 w 3 ) ( x y z ) = ( b 1 b 2 b 3 ) \begin{aligned}
\begin{pmatrix}
u_{1}&v_{1}&w_{1} \\
0&v_{2}&w_{2} \\
0&0&w_{3}
\end{pmatrix}\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}=\begin{pmatrix}
b_{1} \\
b_{2} \\
b_{3}
\end{pmatrix}
\end{aligned} u 1 0 0 v 1 v 2 0 w 1 w 2 w 3 x y z = b 1 b 2 b 3 更进一步,我们可以再通过行变换化简成 reduced echelon form(最简阶梯型) ,此时只有主对角线上有元素,其他都是 0,更便于我们得出解
通解和特解
当进行初等行变换之后出现并非所有列都是主元列,即以下状况:
( u 1 v 1 w 1 0 0 w 2 0 0 w 3 ) ( x y z ) = ( b 1 b 2 b 3 ) \begin{aligned}
\begin{pmatrix}
u_{1}&v_{1}&w_{1} \\
0&0&w_{2} \\
0&0&w_{3}
\end{pmatrix}\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}=\begin{pmatrix}
b_{1} \\
b_{2} \\
b_{3}
\end{pmatrix}
\end{aligned} u 1 0 0 v 1 0 0 w 1 w 2 w 3 x y z = b 1 b 2 b 3 非主元列我们称之为自由变量 ,出现自由变量的时候我们会发现方程不止存在唯一的 solution
你会发现只有 z z z x x x y y y
( x y z ) = ( b 1 − w 1 b 1 w 3 − v 1 y y b 3 w 3 ) = ( b 1 − w 1 b 1 w 3 0 b 3 w 3 ) + y ( − v 1 1 0 ) \begin{pmatrix}
x \\
y \\
z
\end{pmatrix}=\begin{pmatrix}
b_{1}-\frac{w_{1}b_{1}}{w_{3}}-v_{1}y \\
y \\
\frac{b_{3}}{w_{3}}
\end{pmatrix}=\begin{pmatrix}
b_{1}-\frac{w_{1}b_{1}}{w_{3}} \\
0 \\
\frac{b_{3}}{w_{3}}
\end{pmatrix}+y\begin{pmatrix}
-v_{1} \\
1 \\
0
\end{pmatrix} x y z = b 1 − w 3 w 1 b 1 − v 1 y y w 3 b 3 = b 1 − w 3 w 1 b 1 0 w 3 b 3 + y − v 1 1 0 左边那个叫做特解 ,右边那个是方程的通解
注意,加入 b ⃗ = 0 \vec{b}=0 b = 0 零空间的基
线性空间
向量空间
我们通常称满足八大公理的向量集合为向量空间,八大定理如下:
∃ u ⃗ , v ⃗ , z ⃗ , − z ⃗ ∈ V u ⃗ + v ⃗ = v ⃗ + u ⃗ u ⃗ + ( v ⃗ + z ⃗ ) = ( u ⃗ + v ⃗ ) + z ⃗ − z ⃗ + z ⃗ = 0 c ( z ⃗ + u ⃗ ) = c ⃗ z + c ⃗ u c ( d ⃗ z ) = c d ⃗ z ( c + d ) z ⃗ = c ⃗ z + d ⃗ z 0 ⃗ + z ⃗ = z ⃗ 1 ∗ z ⃗ = z ⃗ \begin{aligned}
\exists \vec{u},\vec{v},\vec{z},-\vec{z}\in V\\
\vec{u}+\vec{v}=\vec{v}+\vec{u}
\\
\vec{u}+(\vec{v}+\vec{z})=(\vec{u}+\vec{v})+\vec{z}
\\
-\vec{z}+\vec{z}=0\\
c(\vec{z}+\vec{u})=\vec{c}z+\vec{c}u\\
c(\vec{d}z)=c\vec{d}z\\
(c+d)\vec{z}=\vec{c}z+\vec{d}z\\
\vec{0}+\vec{z}=\vec{z}\\
1*\vec{z}=\vec{z}
\end{aligned} ∃ u , v , z , − z ∈ V u + v = v + u u + ( v + z ) = ( u + v ) + z − z + z = 0 c ( z + u ) = c z + c u c ( d z ) = c d z ( c + d ) z = c z + d z 0 + z = z 1 ∗ z = z 不要小看这些公理,它们是线性代数分析的基石
向量空间中的向量子集如果仍然满足这八大定理,则称这些子集为子空间(subspace) ,否则只能成为子集
我们称 s p a n { a 1 , a 2 , … , a n } span\{a_{1},a_{2},\dots,a_{n}\} s p an { a 1 , a 2 , … , a n } a 1 , a 2 , … , a n a_{1},a_{2},\dots,a_{n} a 1 , a 2 , … , a n ∑ i = 1 n c i a i = 0 \sum_{i=1}^{n}c_{i}a_{i}=0 ∑ i = 1 n c i a i = 0 c i = 0 c_{i}=0 c i = 0 线性独立
(其实这非常好理解,就是空间中任何一个向量都不可能用其他向量表示出来,维度都互不完全一致)
如果这些向量又恰好满足向量空间八大定理,那么我们称这些向量为它们张成的向量空间的基向量
列空间(Column space)
对于以下方程 b ⃗ ≠ 0 \vec{b}\neq 0 b = 0 列空间 ,从另一个角度来说,A 中所有主元列(非主元也可算进去,毕竟维度有重复)向量张成的空间就是列空间(从上文几何角度理解线性变换可以很容易看出来),列空间基的个数=主元列的个数
A x ⃗ = b ⃗ → ( c o l 1 c o l 2 … c o l n ) ( x 1 x 2 . x n ) = b ⃗ A\vec{x}=\vec{b}\to \begin{pmatrix}
col_{1}&col_{2}&\dots&col_{n}
\end{pmatrix}\begin{pmatrix}
x_{1} \\
x_{2} \\
. \\
x_{n}
\end{pmatrix}=\vec{b} A x = b → ( co l 1 co l 2 … co l n ) x 1 x 2 . x n = b 行空间(Row space)
A 中所有行向量所组成的空间我们称为行空间,行空间基的个数=列空间基的个数
如何理解呢?
和列空间分析类似,在化简成 echelon form(阶梯型)之后我们可以发现 pivot column 的个数和 pivot row 的个数其实一致(因为 leading entry 的个数是固定的,而且都是成阶梯型)
( u 1 v 1 w 1 0 0 w 2 0 0 w 3 ) ( x y z ) = ( b 1 b 2 b 3 ) \begin{aligned}
\begin{pmatrix}
u_{1}&v_{1}&w_{1} \\
0&0&w_{2} \\
0&0&w_{3}
\end{pmatrix}\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}=\begin{pmatrix}
b_{1} \\
b_{2} \\
b_{3}
\end{pmatrix}
\end{aligned} u 1 0 0 v 1 0 0 w 1 w 2 w 3 x y z = b 1 b 2 b 3 零空间(Null space)
对于以下方程 b ⃗ = 0 \vec{b}=0 b = 0 零空间 ,可以看回高斯消元法 中 b ⃗ = 0 \vec{b}=0 b = 0 零空间基的个数=自由变量的个数
从几何意义 上来理解,经过线性变换后,空间坍缩成
( u 1 0 0 ) + ( w 1 w 2 w 3 ) \begin{pmatrix}
u_{1} \\
0 \\
0
\end{pmatrix}+\begin{pmatrix}
w_{1} \\
w_{2} \\
w_{3}
\end{pmatrix} u 1 0 0 + w 1 w 2 w 3 这两个向量(把第一个换成第二个列向量 ( v 1 , 0 , 0 ) (v1,0,0) ( v 1 , 0 , 0 )
秩
我们通常用 r a n k ( A ) rank(A) r ank ( A ) d i m ( V ) dim(V) d im ( V )
r a n k ( A ) = d i m ( C o l A ) + d i m ( N u l A ) rank(A)=dim(Col_{A})+dim(Nul_{A}) r ank ( A ) = d im ( C o l A ) + d im ( N u l A ) 因为一个矩阵中的列向量不是主元列就是自由变量,所以我们可以得到列空间基的个数+零空间基的个数=矩阵的列数(n) 或者可以称之为矩阵的维度,因为一般我们都是分析方阵
如果我们说一个矩阵满秩 ,那么代表 r a n k ( A ) = d i m ( C o l A ) rank(A)=dim(Col_{A}) r ank ( A ) = d im ( C o l A ) 可逆 (这里判断通常要通过行变化化简成阶梯型才方便判断,不可以不做任何处理)
基变换
我们现在知道一个向量空间可以用一组基表示,那么向量空间只能有一组基吗?显然不是,我们可以用不同的“基语言”去描述空间中的变化
比如对于二维空间,我们可以用这组标准的向量基(类比普通话)来描述
( 1 0 0 1 ) \begin{pmatrix}
1&0 \\
0&1
\end{pmatrix} ( 1 0 0 1 ) 但是我们也可以用方言(类比粤语)来描述
( 3 1 2 5 ) \begin{pmatrix}
3&1 \\
2&5
\end{pmatrix} ( 3 2 1 5 ) 如果我们用普通话描述了一种线性变换 D D D 先把粤语翻译成普通话,用普通话完成这个线性变换,然后再翻译回粤语,那么就相当于用粤语来描述这种线性变换了
值得注意的是 ,在粤语世界里,我们所说的 ( 1 0 0 1 ) \begin{pmatrix}1&0\\0&1\end{pmatrix} ( 1 0 0 1 ) ( 3 1 2 5 ) \begin{pmatrix}3&1 \\2&5\end{pmatrix} ( 3 2 1 5 )
粤 语 − 1 D 粤语 → ( 3 1 2 5 ) − 1 D ( 3 1 2 5 ) 粤语^{-1}D粤语\to \begin{pmatrix}
3&1 \\
2&5
\end{pmatrix}^{-1}D\begin{pmatrix}
3&1 \\
2&5
\end{pmatrix} 粤 语 − 1 D 粤语 → ( 3 2 1 5 ) − 1 D ( 3 2 1 5 ) 如果这个 D 还是一个对角矩阵的话,这就涉及到了之后会提到的对角化问题 ,我们可以从基变换的角度大大减少计算量
那么对于普通的基变换问题(A 语言转成 B 语言),我们通常探究的是如何用不同语言表达同一个列向量,假设我们有 A , B A,B A , B
A = { a 1 ⃗ , a 2 ⃗ … a n ⃗ } B = { b 1 ⃗ , b 2 ⃗ … b n ⃗ } \begin{aligned}
A=\{\vec{a_{1}},\vec{a_{2}}\dots\vec{a_{n}}\}\\
B=\{\vec{b_{1}},\vec{b_{2}}\dots\vec{b_{n}}\}
\end{aligned} A = { a 1 , a 2 … a n } B = { b 1 , b 2 … b n } 我们在 A A A x ⃗ \vec{x} x
x A ⃗ = ( c 1 c 2 . . c n ) x A ⃗ = c 1 a 1 ⃗ + ⋯ + c n a n ⃗ \begin{aligned}
\vec{x_{A}}=\begin{pmatrix}
c_{1} \\
c_{2} \\
. \\
. \\
c_{n}
\end{pmatrix}\\
\vec{x_{A}}=c_{1}\vec{a_{1}}+\dots+c_{n}\vec{a_{n}}
\end{aligned} x A = c 1 c 2 . . c n x A = c 1 a 1 + ⋯ + c n a n 那么如何在 B 下描述 x ⃗ \vec{x} x A B A_{B} A B a 1 ⃗ ∗ B \vec{a_1}*B a 1 ∗ B a 1 ⃗ B \vec{a_1}_{B} a 1 B
( x A ⃗ ) ∗ B = ( c 1 a ∗ 1 ⃗ + ⋯ + c n a n ⃗ ) B = c 1 ( a 1 B ⃗ + ⋯ + c n a n B ⃗ ) = A B ( c 1 c 2 . . c n ) x B ⃗ = ( d 1 d 2 . . d n ) \begin{aligned}
(\vec{x_{A}})*{B}=(c_{1}\vec{a*{1}}+\dots+c_{n}\vec{a_{n}})_{B}=c_{1}(\vec{a_{1B}}+\dots+c_{n}\vec{a_{nB}})=A_{B}\begin{pmatrix}
c_{1} \\
c_{2} \\
. \\
. \\
c_{n}
\end{pmatrix}\\
\vec{x_{B}}=\begin{pmatrix}
d_{1} \\
d_{2} \\
. \\
. \\
d_{n}
\end{pmatrix}\\
\end{aligned} ( x A ) ∗ B = ( c 1 a ∗ 1 + ⋯ + c n a n ) B = c 1 ( a 1 B + ⋯ + c n a n B ) = A B c 1 c 2 . . c n x B = d 1 d 2 . . d n x A ⃗ \vec{x_{A}} x A x B ⃗ \vec{x_{B}} x B
A B = ( a 1 B ⃗ a 2 B ⃗ … a n B ⃗ ) ( d 1 d 2 . . d n ) = ( a 1 B ⃗ a 2 B ⃗ … a n B ⃗ ) ( c 1 c 2 . . c n ) \begin{aligned}
A_{B}=\begin{pmatrix}
\vec{a_{1B}}&\vec{a_{2B}}&\dots&\vec{a_{nB}}
\end{pmatrix}\\
\begin{pmatrix}
d_{1} \\
d_{2} \\
. \\
. \\
d_{n}
\end{pmatrix}=\begin{pmatrix}
\vec{a_{1B}}&\vec{a_{2B}}&\dots&\vec{a_{nB}}
\end{pmatrix}\begin{pmatrix}
c_{1} \\
c_{2} \\
. \\
. \\
c_{n}
\end{pmatrix}
\end{aligned} A B = ( a 1 B a 2 B … a n B ) d 1 d 2 . . d n = ( a 1 B a 2 B … a n B ) c 1 c 2 . . c n 形象的理解就是,A 语言有一段话,你把 A 语言用 B 语言描述出来,那么输出的就是 B 语言下对这段话的描述
所以关键在于求解 A B A_{B} A B
所以我们可以得到
A B = B − 1 A A_{B}=B^{-1}A A B = B − 1 A 内积
内积通俗来讲就是点乘,u ⃗ ⋅ v ⃗ \vec{u}·\vec{v} u ⋅ v
( u 1 u 2 ) ⋅ ( v 1 v 2 ) = u 1 v 1 + u 2 v 2 + u 3 v 3 = ( u 1 u 2 ) ( v 1 v 2 ) \begin{pmatrix}
u_{1} \\
u_{2} \\
\end{pmatrix}·\begin{pmatrix}
v_{1} \\
v_{2} \\
\end{pmatrix}=u_{1}v_{1}+u_{2}v_{2}+u_{3}v_{3}=\begin{pmatrix}
u_{1}&u_{2}
\end{pmatrix}\begin{pmatrix}
v_{1} \\
v_{2} \\
\end{pmatrix} ( u 1 u 2 ) ⋅ ( v 1 v 2 ) = u 1 v 1 + u 2 v 2 + u 3 v 3 = ( u 1 u 2 ) ( v 1 v 2 ) 其中我们在矩阵相乘时习惯性用转置的符号去书写(其实没什么区别,就是整齐好看罢了),即:
( u 1 u 2 ) T ( v 1 v 2 ) \begin{pmatrix}
u_{1} \\
u_{2} \\
\end{pmatrix}^{T}\begin{pmatrix}
v_{1} \\
v_{2} \\
\end{pmatrix} ( u 1 u 2 ) T ( v 1 v 2 ) 还记得我们在初步认识矩阵 章节中提到的将矩阵看成线性变换 吗?
同理,在这里我们把 ( u 1 u 2 ) \begin{pmatrix}u_{1}&u_{2}\end{pmatrix} ( u 1 u 2 ) 这个变换是线性的吗,如何看这个坍缩的过程?
我们在空间中定义一个全新的倾斜的数轴,空间中的向量或者点投射到这个数轴上的变换就是一个坍缩的过程。由于空间中等距的点投射到这个数轴上仍然等距,原点不动,所以这样的坍缩变换仍然是线性变换
( u 1 u 2 ) \begin{pmatrix}u_{1}&u_{2}\end{pmatrix} ( u 1 u 2 ) ( v 1 v 2 ) \begin{pmatrix}v_{1}\\v_{2}\end{pmatrix} ( v 1 v 2 )
具体如何理解投射的过程呢? 我们定义一个单位向量 u ⃗ = ( u x , u y ) \vec{u}=(u_{x},u_{y}) u = ( u x , u y ) u ⃗ \vec{u} u u x u_{x} u x u y u_{y} u y u x 或者 u y u_{x}或者u_{y} u x 或者 u y
v ⃗ ⋅ u ⃗ = v x u x + v y u y \vec{v}·\vec{u}=v_{x}u_{x}+v_{y}u_{y} v ⋅ u = v x u x + v y u y 那么对于任意两两向量的内积,就可以先把一个向量变成单位向量 ,进行内积之后乘上模长即可
我们得到公式:
v ⃗ ⋅ u ⃗ = ∣ ∣ v ⃗ ∣ ∣ ∗ ∣ ∣ u ⃗ ∣ ∣ ∗ < v ⃗ , u ⃗ > \vec{v}·\vec{u}=| |\vec{v}| |*|
|\vec{u}| |*<\vec{v},\vec{u}> v ⋅ u = ∣∣ v ∣∣ ∗ ∣∣ u ∣∣ ∗ < v , u > 那为什么内积的先后顺序不影响内积结果呢?
矩阵的线性变换和乘积先后有关系,但是为什么内积的结果就和乘积先后无关呢?
我们可以直接从上面推导出来的式子得出,不管把哪个先处理成单位向量,乘积大小都和顺序无关(无非就是把刚刚的 u ⃗ \vec{u} u v ⃗ \vec{v} v
广义内积 (投影变换)
刚刚我们理解了两个列向量之间的内积,接下来我们推广到矩阵与矩阵之间的内积
A ⋅ B = A T B A·B=A^TB A ⋅ B = A T B 我们一样可以通过投射的思想来理解这件事情,举个具体的例子
( 1 2 3 4 ) ⋅ ( 3 4 5 6 ) = ( 1 3 2 4 ) ( 3 4 5 6 ) \begin{pmatrix}
1&2 \\
3&4
\end{pmatrix}·\begin{pmatrix}
3&4 \\
5&6
\end{pmatrix}=\begin{pmatrix}
1&3 \\
2&4
\end{pmatrix}\begin{pmatrix}
3&4 \\
5&6
\end{pmatrix} ( 1 3 2 4 ) ⋅ ( 3 5 4 6 ) = ( 1 2 3 4 ) ( 3 5 4 6 ) 这里相当于先把 ( 1 3 2 4 ) \begin{pmatrix}1&3\\2&4\end{pmatrix} ( 1 2 3 4 ) ( 1 3 ) \begin{pmatrix}1&3\end{pmatrix} ( 1 3 ) ( 2 4 ) \begin{pmatrix}2&4\end{pmatrix} ( 2 4 ) ( 3 5 ) \begin{pmatrix}3\\5\end{pmatrix} ( 3 5 ) ( 4 6 ) \begin{pmatrix}4\\6\end{pmatrix} ( 4 6 ) ( 1 3 ) \begin{pmatrix}1&3\end{pmatrix} ( 1 3 ) ( 2 4 ) \begin{pmatrix}2&4\end{pmatrix} ( 2 4 )
( 1 ∗ 3 + 3 ∗ 5 1 ∗ 4 + 3 ∗ 6 2 ∗ 3 + 4 ∗ 5 2 ∗ 4 + 4 ∗ 6 ) = ( 18 22 26 32 ) = ( 10 ∗ 18 10 10 ∗ 22 10 20 ∗ 26 20 20 ∗ 32 20 ) = ( 10 0 0 20 ) ( 18 10 22 10 26 20 32 20 ) \begin{aligned}
\begin{pmatrix}
1*3+3*5&1*4+3*6 \\
2*3+4*5&2*4+4*6
\end{pmatrix}
\\=\begin{pmatrix}
18&22 \\
26&32
\end{pmatrix}
\\=\begin{pmatrix}
\sqrt{ 10 }*\frac{18}{\sqrt{ 10 }}&\sqrt{ 10 }*\frac{22}{\sqrt{ 10 }} \\
\sqrt{ 20 }*\frac{26}{\sqrt{ 20 }}&\sqrt{ 20 }*\frac{32}{\sqrt{ 20 }}
\end{pmatrix}
\\=\begin{pmatrix}
\sqrt{ 10 }&0 \\
0&\sqrt{ 20 }
\end{pmatrix}\begin{pmatrix}
\frac{{18}}{\sqrt{ 10 }}&\frac{22}{\sqrt{ 10 }} \\
\frac{26}{\sqrt{ 20 }}& \frac{32}{\sqrt{ 20 }}
\end{pmatrix}
\end{aligned} ( 1 ∗ 3 + 3 ∗ 5 2 ∗ 3 + 4 ∗ 5 1 ∗ 4 + 3 ∗ 6 2 ∗ 4 + 4 ∗ 6 ) = ( 18 26 22 32 ) = ( 10 ∗ 10 18 20 ∗ 20 26 10 ∗ 10 22 20 ∗ 20 32 ) = ( 10 0 0 20 ) ( 10 18 20 26 10 22 20 32 ) 从这个角度也可以体会到矩阵相乘的另外一层意义,从向量方程入手 一章我们讲了从拉伸转动坐标系的角度理解矩阵相乘,而内积 这一小节告诉我们可以从投射的角度理解矩阵相乘和矩阵转置 :先做投射,把投射数轴形成新的坐标系,表示出在新投影坐标系中原来向量的坐标(注意这里的坐标大小是投影大小而不是平行过去 ),然后把新坐标系的单位长度拉长为被投射向量模长,我们姑且把这个变换叫做投射变换 吧
特征向量、特征值与对角化
通常我们通过这样一个式子初步理解特征向量(规定 x ⃗ ≠ 0 \vec{x}\neq 0 x = 0
A x ⃗ = λ x ⃗ A\vec{x}=\lambda\vec{x} A x = λ x 对于一个矩阵 A A A λ i , x ⃗ i \lambda_{i},\vec{x}_{i} λ i , x i x ⃗ \vec{x} x I I I
( A − λ I ) x ⃗ = 0 (A-\lambda I)\vec{x}=0 ( A − λ I ) x = 0 如果 ( A − λ I ) (A-\lambda I) ( A − λ I ) x ⃗ = 0 ⃗ \vec{x}=\vec{0} x = 0 x ⃗ \vec{x} x 0 ⃗ \vec{0} 0 x ⃗ \vec{x} x ( A − λ I ) (A-\lambda I) ( A − λ I ) x ⃗ \vec{x} x 0 ⃗ \vec{0} 0 0 ⃗ \vec{0} 0
∣ A − λ I ∣ = 0 \begin{vmatrix}
A-\lambda I
\end{vmatrix}=0 A − λ I = 0 知道 λ \lambda λ λ \lambda λ x ⃗ \vec{x} x ( 2 0 0 2 ) \begin{pmatrix}2&0\\0&2\end{pmatrix} ( 2 0 0 2 )
为了更方便地去表示变换后仍然共线的向量,所以我们提取最大公因数后把公共向量表达特征向量
(从另一个角度来说就是对同一个 λ \lambda λ 基向量 作为最终的特征向量结果)
对于不同的 λ \lambda λ
A x 1 ⃗ = λ 1 x 1 ⃗ A x 2 ⃗ = λ 2 x 2 ⃗ i f f c 1 , c 2 = 0 , l e t c 1 x 1 ⃗ + c 2 x 2 ⃗ = 0 p r o o f : A ( c 1 x 1 ⃗ + c 2 x 2 ⃗ ) = λ 1 c 1 x 1 ⃗ + λ 2 c 2 x 2 ⃗ = 0 λ 1 c 1 x 1 + λ 1 c 2 x 2 ⃗ ⃗ = 0 u p − d o w n = ( λ 2 − λ 1 ) c 2 x 2 ⃗ = 0 B e c a u s e λ 2 ≠ λ 1 , x 2 ⃗ ≠ ⃗ 0 S o c 2 = 0 \begin{aligned}
A\vec{x_{1}}=\lambda_{1}\vec{x_{1}}\\
A\vec{x_{2}}=\lambda_{2}\vec{x_{2}}\\
iff c_{1},c_{2}=0,let\\
c_{1}\vec{x_{1}}+c_{2}\vec{x_{2}}=0\\
proof:\\
A(c_{1}\vec{x_{1}}+c_{2}\vec{x_{2}})=\lambda_{1}c_{1}\vec{x_{1}}+\lambda_{2}c_{2}\vec{x_{2}}=0\\
\lambda_{1}c_{1}\vec{x_{1}+\lambda_{1}c_{2}\vec{x_{2}}}=0\\
up-down=(\lambda_{2}-\lambda_{1})c_{2}\vec{x_{2}}=0\\
Because\\\lambda_{2}\neq \lambda_{1},\vec{x_{2}}\vec{\neq}0\\
So\\c_{2}=0\\
\end{aligned} A x 1 = λ 1 x 1 A x 2 = λ 2 x 2 i ff c 1 , c 2 = 0 , l e t c 1 x 1 + c 2 x 2 = 0 p roo f : A ( c 1 x 1 + c 2 x 2 ) = λ 1 c 1 x 1 + λ 2 c 2 x 2 = 0 λ 1 c 1 x 1 + λ 1 c 2 x 2 = 0 u p − d o w n = ( λ 2 − λ 1 ) c 2 x 2 = 0 B ec a u se λ 2 = λ 1 , x 2 = 0 S o c 2 = 0 c 1 c_{1} c 1 λ \lambda λ λ \lambda λ 特征空间(Eigen-space)
特征向量、特征值与对角化的关系
假如 A A A
( a 0 0 0 b 0 0 0 c ) \begin{pmatrix}
a&0&0 \\
0&b&0 \\
0&0&c
\end{pmatrix} a 0 0 0 b 0 0 0 c 它表示的意思就是每个维度伸长 a/b/c 倍,这意味着特征值就是 a, b, c(这可以从行列式=0 的角度理论性地理解;也可以从几何上来看,刚好在坐标轴上的向量伸长对应的倍数)
在对角化矩阵乘法中,我们可以尝到简便计算的甜头:
( a 0 0 0 b 0 0 0 c ) n ( x y z ) = ( a n x 0 0 0 b n y 0 0 0 c n z ) \begin{aligned}
\begin{pmatrix}
a&0&0 \\
0&b&0 \\
0&0&c
\end{pmatrix}^{n}\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}=\begin{pmatrix}
a^{n}x&0&0 \\
0&b^{n}y&0 \\
0&0&c^{n}z
\end{pmatrix}
\end{aligned} a 0 0 0 b 0 0 0 c n x y z = a n x 0 0 0 b n y 0 0 0 c n z 但如果矩阵不是对角矩阵,而且还要做很多次乘法,这怎么办?
A n ( e f g ) = ? A^{n}\begin{pmatrix}
e \\
f \\
g
\end{pmatrix}=? A n e f g = ? 为了更加具象化好理解,这里举特定的例子
A = ( 3 1 0 2 ) A=\begin{pmatrix}
3&1 \\
0&2
\end{pmatrix} A = ( 3 0 1 2 ) 我们得到它的特征值和特征向量为
λ 1 = 3 , x 1 ⃗ = ( 1 0 ) λ 2 = 2 , x 2 ⃗ = ( 1 − 1 ) \begin{aligned}
\lambda_{1}=3,\vec{x_{1}}=\begin{pmatrix}
1 \\
0
\end{pmatrix}\\
\lambda_{2}=2,\vec{x_{2}}=\begin{pmatrix}
1 \\
-1
\end{pmatrix}
\end{aligned} λ 1 = 3 , x 1 = ( 1 0 ) λ 2 = 2 , x 2 = ( 1 − 1 ) 我们可以把矩阵对角化,然后做乘法
还记得我们上文提到过的基变换 吗,这时候我们可以用特征空间中的特征向量(如果数量足够,即特征空间的维度 ≥ \geq ≥ 换个坐标系 ,但本质上 A 的伸拉操作并没有改变。此时
( 1 1 0 − 1 ) − 1 ( 3 1 0 2 ) ( 1 1 0 − 1 ) = ( 3 0 0 2 ) \begin{aligned}
\begin{pmatrix}
1&1 \\
0&-1
\end{pmatrix}^{-1}\begin{pmatrix}
3&1 \\
0&2
\end{pmatrix}\begin{pmatrix}
1&1 \\
0&-1
\end{pmatrix}=\begin{pmatrix}
3&0 \\
0&2
\end{pmatrix}
\end{aligned} ( 1 0 1 − 1 ) − 1 ( 3 0 1 2 ) ( 1 0 1 − 1 ) = ( 3 0 0 2 ) 对 A 的对角化操作 ,就是把式子变换一下,变成:
( 3 1 0 2 ) = ( 1 1 0 − 1 ) ( 3 0 0 2 ) ( 1 1 0 − 1 ) − 1 \begin{pmatrix}
3&1 \\
0&2
\end{pmatrix}=\begin{pmatrix}
1&1 \\
0&-1
\end{pmatrix}\begin{pmatrix}
3&0 \\
0&2
\end{pmatrix}\begin{pmatrix}
1&1 \\
0&-1
\end{pmatrix}^{-1} ( 3 0 1 2 ) = ( 1 0 1 − 1 ) ( 3 0 0 2 ) ( 1 0 1 − 1 ) − 1 这样就可以对 A n A^{n} A n 约束条件 :
d i m A = d i m ( E i g e n − s p a c e ) di mA=di m(Eigen-space) d im A = d im ( E i g e n − s p a ce ) 如果特征空间的维度低于 A 的维度,那么意味着无法用特征向量去表征 A 所在的空间
这里引入一个相似 的概念:A 如果能对角化得到对角矩阵 B,那么则称 A 与 B 互为相似矩阵 (这很好理解,A 表示的在标准基下的变换 等效于 B 表示的在特征基下的变换 ,所以它俩相似)
正交与对角
对于向量空间中的一组基 B = { b 1 ⃗ , b 2 ⃗ , b 3 ⃗ … b n ⃗ } B=\{\vec{b_{1}},\vec{b_{2}},\vec{b_{3}}\dots \vec{b_{n}}\} B = { b 1 , b 2 , b 3 … b n }
∀ b i ⃗ , b j ⃗ i n B , b i ⃗ ⋅ b j ⃗ = 0 T h e n w e c a l l B a s o r t h o g o n a l b a s i s \begin{aligned}
\forall \vec{b_{i}},\vec{b_{j}}inB,\\
\vec{b_{i}}·\vec{b_{j}}=0\\
Then \, we \,ca l l \, B \,as \, ort hogona l \,basis
\end{aligned} ∀ b i , b j in B , b i ⋅ b j = 0 T h e n w e c a ll B a s or t h o g o na l ba s i s 也就是说正交基中向量都互相垂直,显然它们互相线性独立(验证是否线性独立就一个方法:当且仅当所有 c i = 0 c_{i}=0 c i = 0 ∑ i = 1 n c i b i ⃗ = 0 \sum_{i=1}^{n}c_{i}\vec{b_{i}}=0 ∑ i = 1 n c i b i = 0 标准正交基
如果把这组基写成矩阵的形式,而且规定 ∣ ∣ b i ⃗ ∣ ∣ = 1 , B ∈ R n ∗ n | |\vec{b_{i}}| |=1,B\in R^{n*n} ∣∣ b i ∣∣ = 1 , B ∈ R n ∗ n
了解了空间中正交矩阵的概念,我们不难理解以下性质(用< u ⃗ , v ⃗ \vec{u},\vec{v} u , v
B T ⋅ B = B ⋅ B T = I B T = B − 1 < B x ⃗ , B y ⃗ > = < x ⃗ , y ⃗ > ∣ ∣ B x ⃗ ∣ ∣ = ∣ ∣ x ⃗ ∣ ∣ \begin{aligned}
B^{T}·B=B·B^T=I\\
B^T=B^{-1}\\
<B\vec{x},B\vec{y}> = <\vec{x},\vec{y}>\\
| |B\vec{x}| |=| |\vec{x}| |
\end{aligned} B T ⋅ B = B ⋅ B T = I B T = B − 1 < B x , B y >=< x , y > ∣∣ B x ∣∣ = ∣∣ x ∣∣ 做线性变换 B 相当于旋转平移坐标轴,这不会改变两个向量之间的夹角和向量的模长。教科书中常常写的是 B T x ⃗ B^{T}\vec{x} B T x B T B^T B T B B B
正交化
在大多数情况下,向量空间中我们已知的基都比较“草率”,我们需要对它们进行规范化处理,即把它们变成正交基,写成正交矩阵形式。这个正交化的过程我们叫做格拉姆-施密特正交化(Gram-Schmit Process)
简单来说,这是一个做投影的过程,我们现在手头有一组无规则的基 A = { a 1 ⃗ , a 2 ⃗ , a 3 ⃗ … a n ⃗ } A=\{\vec{a_{1}},\vec{a_{2}},\vec{a_{3}}\dots \vec{a_{n}}\} A = { a 1 , a 2 , a 3 … a n } B = { b 1 ⃗ , b 2 ⃗ , b 3 ⃗ … b n ⃗ } B=\{\vec{b_{1}},\vec{b_{2}},\vec{b_{3}}\dots \vec{b_{n}}\} B = { b 1 , b 2 , b 3 … b n } b 1 ⃗ = a 1 ⃗ \vec{b_{1}}=\vec{a_{1}} b 1 = a 1 b 2 ⃗ = a 2 ⃗ − < a 2 ⃗ , b 1 ∣ ∣ b 1 ⃗ ∣ ∣ ⃗ > ∗ b 1 ∣ ∣ b 1 ⃗ ∣ ∣ ⃗ \vec{b_{2}}=\vec{a_{2}}-<\vec{a_{2}},\vec{\frac{b_{1}}{| |\vec{b_{1}}| |}}>*\vec{\frac{b_{1}}{| |\vec{b_{1}}| |}} b 2 = a 2 − < a 2 , ∣∣ b 1 ∣∣ b 1 > ∗ ∣∣ b 1 ∣∣ b 1 b i ⃗ \vec{b_{i}} b i 第 i 个向量 a i ⃗ \vec{a_{i}} a i a i ⃗ \vec{a_{i}} a i ,这样不断循环最终可以得到一组正交基
这可以用一个循环程序的思想来叙述:
b 1 ⃗ = a 1 ⃗ f o r ( k = 2 ; k < n + 1 ; k + + ) { b k ⃗ = a k ⃗ − ∑ i = 1 k − 1 < b i , a k ⃗ > b i ⃗ , b k ⃗ = b k ⃗ ∣ ∣ b k ⃗ ∣ ∣ } \begin{aligned}
\vec{b_{1}}=\vec{a_{1}}\\
for (k=2; k<n+1;k++)\\
\left\{ \\
\vec{b_{k}}=\vec{a_{k}}-\sum_{i=1}^{k-1}<\vec{b_{i},a_{k}}>\vec{b_{i}}\\,
\vec{b_{k}}=\frac{\vec{b_{k}}}{| |\vec{b_{k}}| |}
\right\}
\end{aligned} b 1 = a 1 f or ( k = 2 ; k < n + 1 ; k + + ) { b k = a k − i = 1 ∑ k − 1 < b i , a k > b i , b k = ∣∣ b k ∣∣ b k } (这可能看上去很复杂,其实就是对上面加粗的话用数学语言来表示,注意这里均对 b i ⃗ \vec{b_{i}} b i a k ⃗ \vec{a_{k}} a k a k ⃗ \vec{a_{k}} a k
对式子进行移项,我们可以得到
a k ⃗ = b k ⃗ + ∑ i = 1 k − 1 < b i ∣ ∣ b i ⃗ ∣ ∣ , a k ⃗ > ( b i ⃗ ∣ ∣ b i ⃗ ∣ ∣ ) \vec{a_{k}}=\vec{b_{k}}+\sum_{i=1}^{k-1}<\vec{\frac{b_{i}}{| |\vec{b_{i}}| |},a_{k}}>\left( \frac{\vec{b_{i}}}{| |\vec{b_{i}}| |} \right) a k = b k + i = 1 ∑ k − 1 < ∣∣ b i ∣∣ b i , a k > ( ∣∣ b i ∣∣ b i ) 用矩阵来表示:
QR 分解
通常求 QR 分解的思路是先把所有的正交基求出来,再写出分解矩阵
正交对角化
前文我们提到对角化,就是以下的一个过程:
A = P D P − 1 A=PDP^{-1} A = P D P − 1 如果此时的 P T = P − 1 P^T=P^{-1} P T = P − 1 A A A D D D 合同变换 (其实这个名字并不是很好理解,不如记成正交对角化):
A = P D P T A=PDP^T A = P D P T 从本质上来讲,就是 A 的特征向量组成的基刚好是一组正交基
P − 1 A P = D P^{-1}AP=D P − 1 A P = D 此时我们对 A A A
P − 1 A = P T A = D P T ( P T A ) T = ( D P T ) T A T P = P D T = P D A T = P D P − 1 = P D P T = A \begin{aligned}
P^{-1}A=P^TA=DP^T\\
(P^TA)^T=(DP^T)^T\\
A^TP=PD^T=PD\\
A^T=PDP^{-1}=PDP^T=A
\end{aligned} P − 1 A = P T A = D P T ( P T A ) T = ( D P T ) T A T P = P D T = P D A T = P D P − 1 = P D P T = A 所以我们得到 A 的转置矩阵还是 A ,我们称这种矩阵为对称矩阵
那反过来看,如果 A T = A A^T=A A T = A P P P D D D 关键所在就是 A T = A A^T=A A T = A ,如果大于等于就说明可以对角化,再根据 A T = A A^T=A A T = A
A x ⃗ = λ x ⃗ A \vec{x}=\lambda \vec{x} A x = λ x 首先对称矩阵意味着它是一个方阵,A ∈ R n ∗ n A\in R^{n*n} A ∈ R n ∗ n A T = A A^T=A A T = A 特殊的例子 来帮助理解(坐标系对角压缩,就是两个基向量对称靠近的过程)
我们可以找到两个特征向量 (至于怎么找的可以拿一个具体类似的矩阵去验证一下),这两个特征向量在纯坐标系转换视角下的坐标和在投射变换视角下的坐标大小一致,标同样颜色的两两互相相等。更推广地来说,如果把基向量拉长,整体空间都是线性拉长,所以两种转换视角出来一样等效。我们在两种转换等效的情况下可以找到充足的特征向量去表征 A 的维度
我们在研究数学问题时常常碰到非线性规划问题,求解一个多元二次函数的最值,比如:
x ⃗ = ( x 1 x 2 x 3 . . x n ) f ( x ⃗ ) = ∑ i = 1 , j = 1 n c i j x i x j \begin{aligned}
\vec{x}=\begin{pmatrix}
x_{1} \\
x_{2} \\
x_{3} \\
. \\
. \\
x_{n}
\end{pmatrix}\\
f(\vec{x})=\sum_{i=1,j=1}^{n}c_{ij}x_{i}x_{j}
\end{aligned} x = x 1 x 2 x 3 . . x n f ( x ) = i = 1 , j = 1 ∑ n c ij x i x j 通常我们求解的是 f ( x ⃗ ) f(\vec{x}) f ( x )
( x 1 x 2 … x n ) ( c 11 c 21 … c n 1 c 12 . . c 1 n c 2 n … c n n ) ( x 1 x 2 . . x n ) \begin{pmatrix}
x_{1}&x_{2}&\dots&x_{n}
\end{pmatrix}\begin{pmatrix}
c_{11}&c_{21}&\dots&c_{n_{1}} \\
c_{12} \\
. \\
. \\
c_{1n}&c_{2n}&\dots&c_{nn}
\end{pmatrix}\begin{pmatrix}
x_{1} \\
x_{2} \\
. \\
. \\
x_{n}
\end{pmatrix} ( x 1 x 2 … x n ) c 11 c 12 . . c 1 n c 21 c 2 n … … c n 1 c nn x 1 x 2 . . x n 由于 c i j x i x j c_{ij}x_{i}x_{j} c ij x i x j c j i x j x i c_{ji}x_{j}x_{i} c ji x j x i
( x 1 x 2 … x n ) ( c 11 c 12 2 … c 1 n 2 c 12 2 . . c 1 n 2 c 2 n 2 … c n n ) ( x 1 x 2 . . x n ) \begin{pmatrix}
x_{1}&x_{2}&\dots&x_{n}
\end{pmatrix}\begin{pmatrix}
c_{11}&\frac{c_{12}}{2}&\dots&\frac{c_{1n}}{2} \\
\frac{c_{12}}{2} \\
. \\
. \\
\frac{c_{1n}}{2}&\frac{c_{2n}}{2}&\dots&c_{nn}
\end{pmatrix}\begin{pmatrix}
x_{1} \\
x_{2} \\
. \\
. \\
x_{n}
\end{pmatrix} ( x 1 x 2 … x n ) c 11 2 c 12 . . 2 c 1 n 2 c 12 2 c 2 n … … 2 c 1 n c nn x 1 x 2 . . x n 这时候我们注意到中间那个矩阵是一个对称矩阵,而左右两边的矩阵互为转置关系(这其实有点像正交对角化的样子,但不是哈)
因此我们可以把函数写成:
f ( x ⃗ ) = x ⃗ T D x ⃗ f(\vec{x})=\vec{x}^TD \vec{x} f ( x ) = x T D x 我们定义对称矩阵 D D D 。 由于 D D D D D D 根据特征值和对角化关系,G 中的每一个非零元素就是矩阵 D 的特征值,P 就是特征向量组成的矩阵 (要是不理解就看回特征向量那一章)
D = P G P T D=PGP^T D = PG P T 带入到函数中,我们可以得到:
f ( x ⃗ ) = x ⃗ T P G P T x ⃗ = ( P T x ⃗ ) T G ( P T x ⃗ ) = y ⃗ T G y ⃗ = ( y 1 y 2 … y n ) G ( y 1 y 2 . . y n ) = ∑ i = 1 n λ i y i 2 \begin{aligned}
f(\vec{x})=\vec{x}^TPGP^T \vec{x}=(P^T \vec{x})^TG(P^T \vec{x})=\vec{y}^TG \vec{y}
\\=\begin{pmatrix}
y_{1}&y_{2}&\dots&y_{n}\end{pmatrix}G\begin{pmatrix}
y_{1} \\
y_{2} \\
. \\
. \\
y_{n}
\end{pmatrix}=\sum_{i=1}^{n}\lambda_{i}y_{i}^2
\end{aligned} f ( x ) = x T PG P T x = ( P T x ) T G ( P T x ) = y T G y = ( y 1 y 2 … y n ) G y 1 y 2 . . y n = i = 1 ∑ n λ i y i 2
λ i \lambda_{i} λ i ∣ ∣ y ⃗ ∣ ∣ = ∣ ∣ x ⃗ ∣ ∣ | |\vec{y}| |=| |\vec{x}| | ∣∣ y ∣∣ = ∣∣ x ∣∣ 如果 λ i \lambda_{i} λ i y i y_{i} y i
如果 ∀ λ i > 0 \forall \lambda_{i}> 0 ∀ λ i > 0 正定阵 ,若 ∀ λ i < 0 \forall \lambda_{i}< 0 ∀ λ i < 0 负定阵 ,其余情况下叫做不定矩阵,这个通常用于求最小值或者最大值(在 y i = 0 y_{i}=0 y i = 0
在实际做题中,我们通常使用配方法(配成 ( x i + x j ) 2 (x_{i}+x_{j})^2 ( x i + x j ) 2 λ i \lambda_{i} λ i
结语
如果你认真看到了这里,那么恭喜你,你对线性代数的理解更加深入了。这些几何意义上的理解看似对做题正确率没有什么太大的意义,但对将来我们学习概率论,泛函分析等打下坚实的基础。密密麻麻的证明公式不一定记得住,但简约的几何印象一定会深深印刻在我们的脑海里。
-----24 级大一小登 W J s i l e n c e − b r e a k e r WJ_{silence-br eaker} W J s i l e n ce − b re ak er
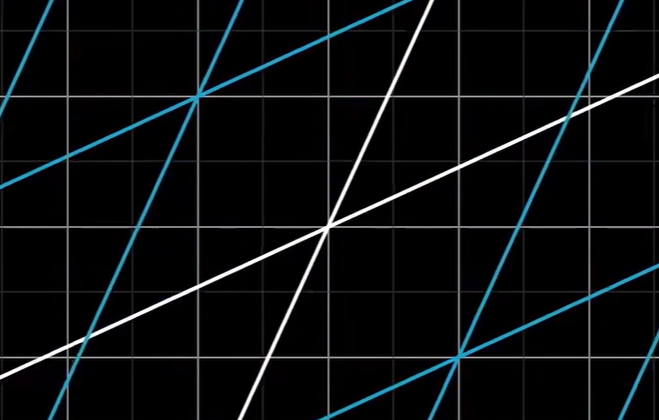 更广义地去说线性变换,我们常常定义 ,称 为对向量 的线性变换,它满足以下公理:
更广义地去说线性变换,我们常常定义 ,称 为对向量 的线性变换,它满足以下公理: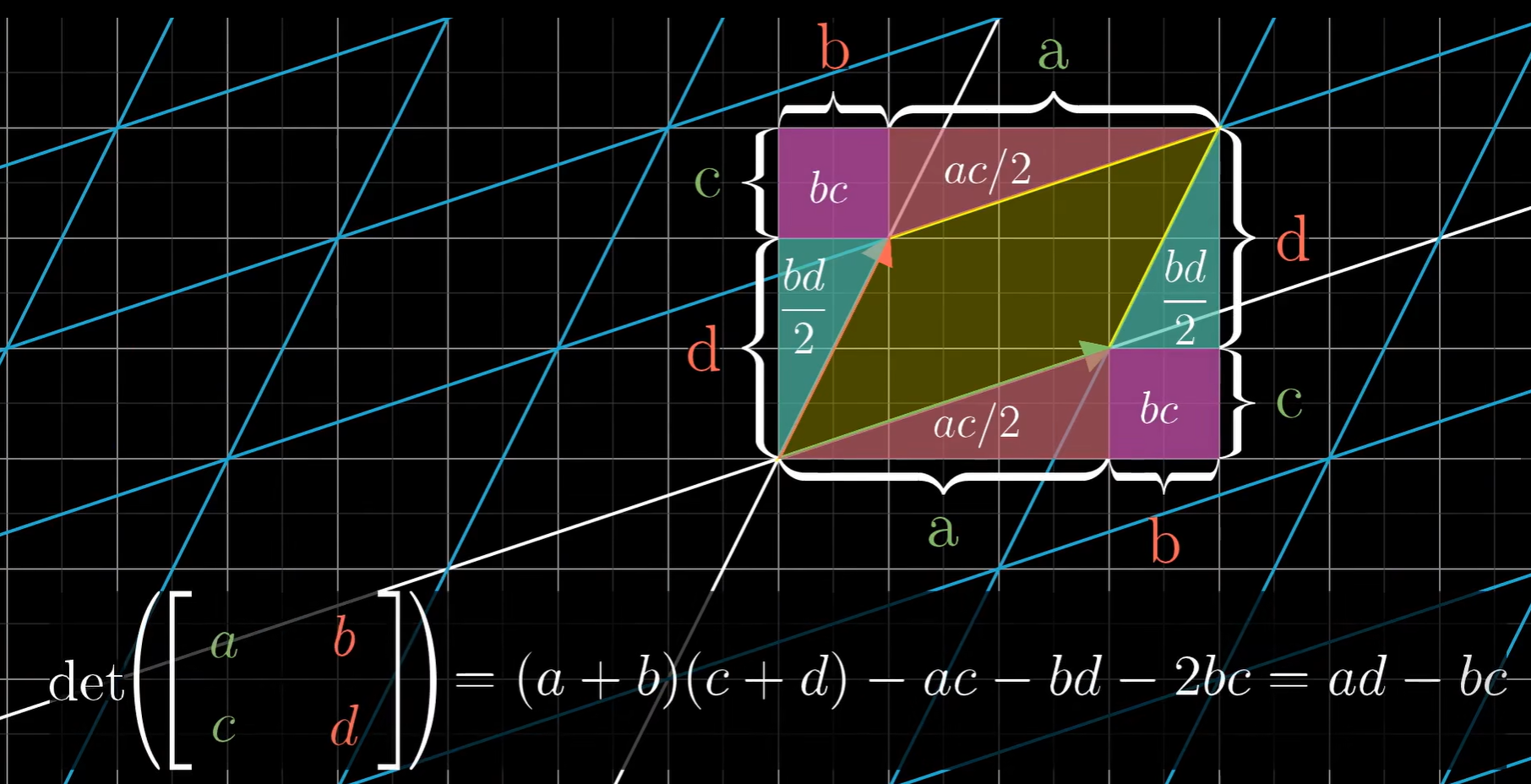 那么行列式是负数的情况怎么理解呢,这可以看成两个向量本来是右手系,但是线性变换后变成了左手系,表示另一边的面积,所以取负号,可以区分
通过建立行列式的几何印象理解后,我们很容易理解为什么只有 n* n 阶行列式,而且我们不难发现可以对行列式性质一眼盯真:
那么行列式是负数的情况怎么理解呢,这可以看成两个向量本来是右手系,但是线性变换后变成了左手系,表示另一边的面积,所以取负号,可以区分
通过建立行列式的几何印象理解后,我们很容易理解为什么只有 n* n 阶行列式,而且我们不难发现可以对行列式性质一眼盯真: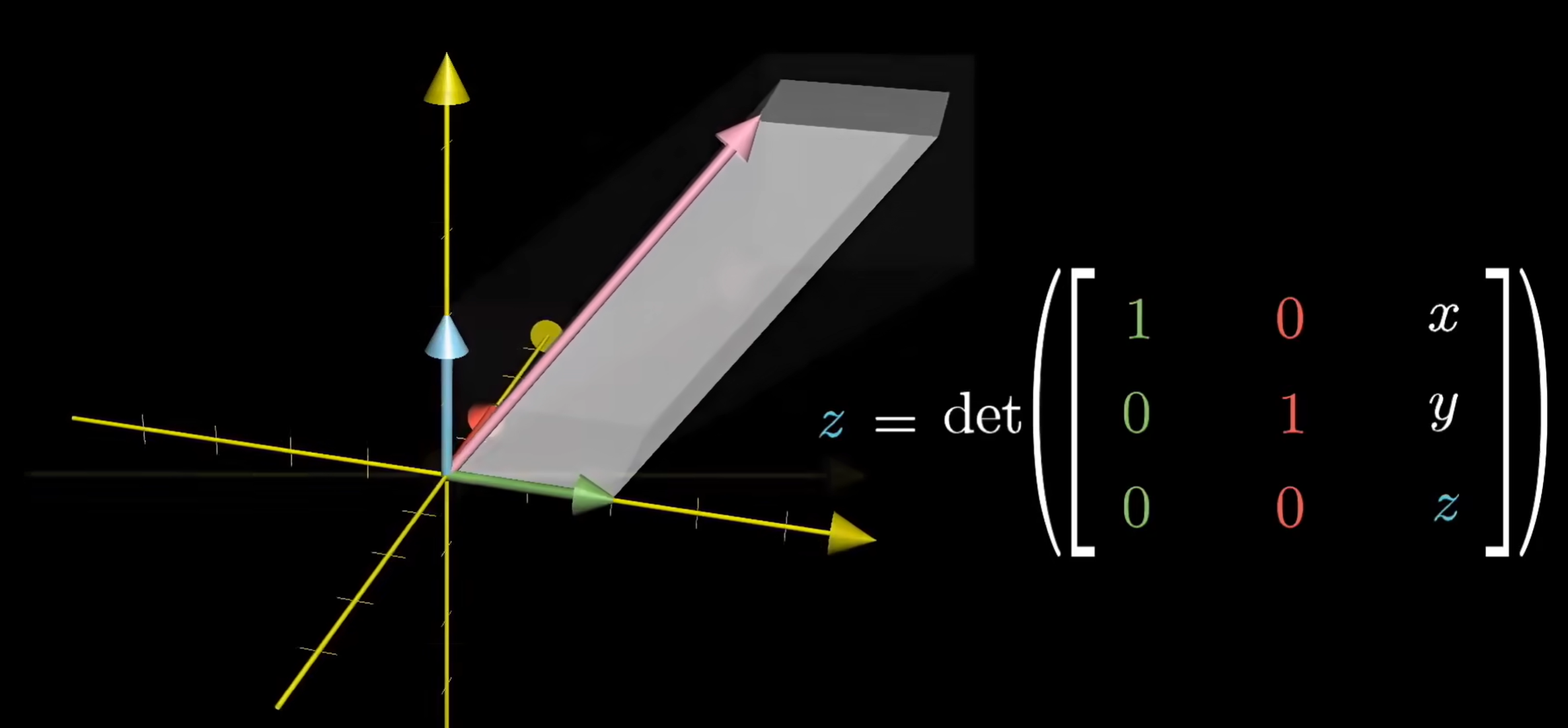 以求 x 为例:
经过线性变换后
以求 x 为例:
经过线性变换后
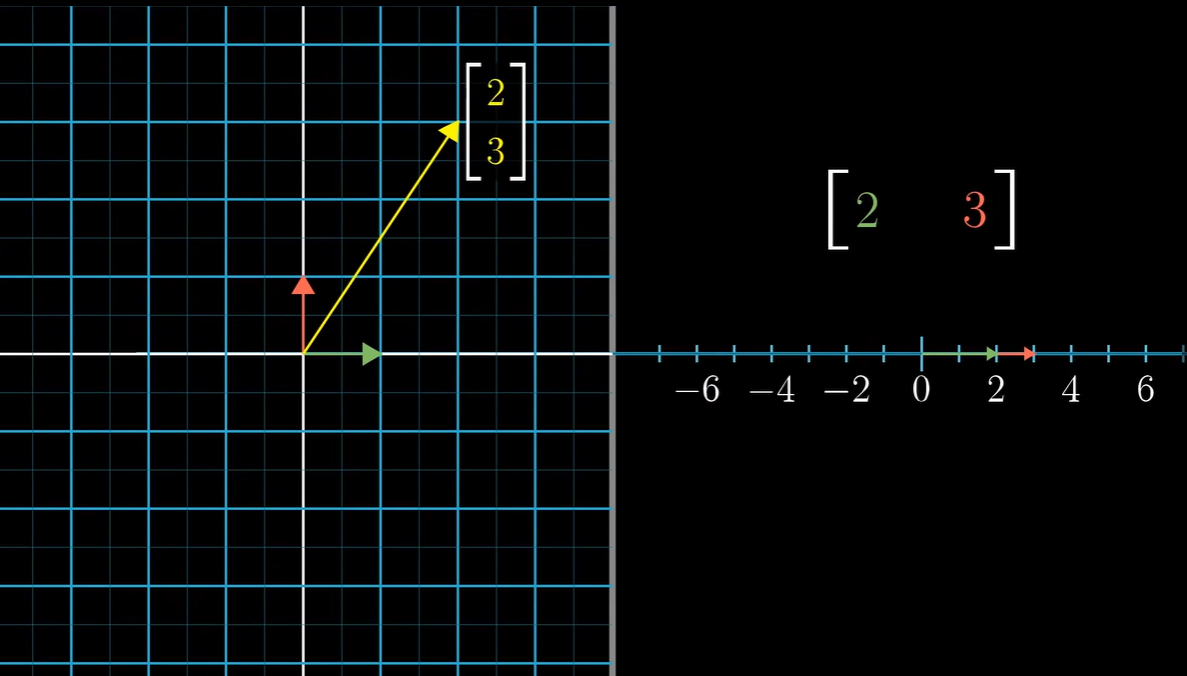 这个变换是线性的吗,如何看这个坍缩的过程?
我们在空间中定义一个全新的倾斜的数轴,空间中的向量或者点投射到这个数轴上的变换就是一个坍缩的过程。由于空间中等距的点投射到这个数轴上仍然等距,原点不动,所以这样的坍缩变换仍然是线性变换
这个变换是线性的吗,如何看这个坍缩的过程?
我们在空间中定义一个全新的倾斜的数轴,空间中的向量或者点投射到这个数轴上的变换就是一个坍缩的过程。由于空间中等距的点投射到这个数轴上仍然等距,原点不动,所以这样的坍缩变换仍然是线性变换
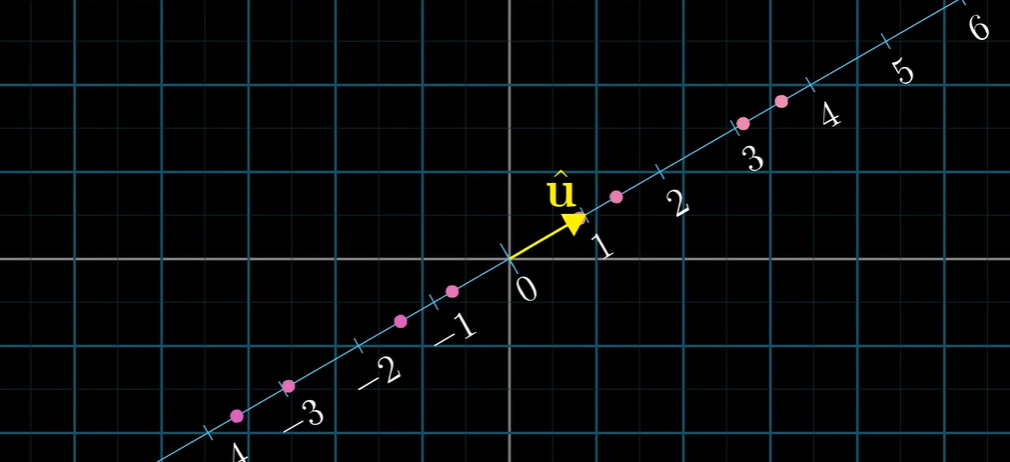 所以内积就可以看成一个向量往一个倾斜数轴上投射的坍缩变换的过程,我们通过 这个矩阵找出投射数轴,然后将 投射到这个数轴上,投射得到的一维向量就是我们想要的结果(因为是一维向量所以就可以看成一个标量数字了)
所以内积就可以看成一个向量往一个倾斜数轴上投射的坍缩变换的过程,我们通过 这个矩阵找出投射数轴,然后将 投射到这个数轴上,投射得到的一维向量就是我们想要的结果(因为是一维向量所以就可以看成一个标量数字了)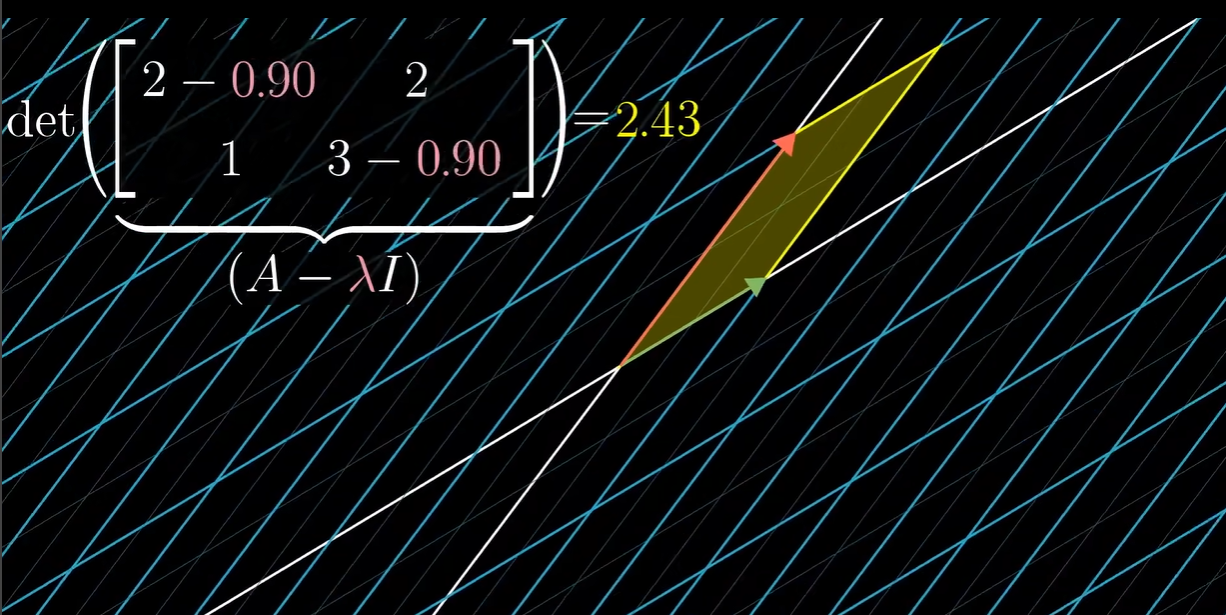 所以我们计算特征值的时候就相当于求解
所以我们计算特征值的时候就相当于求解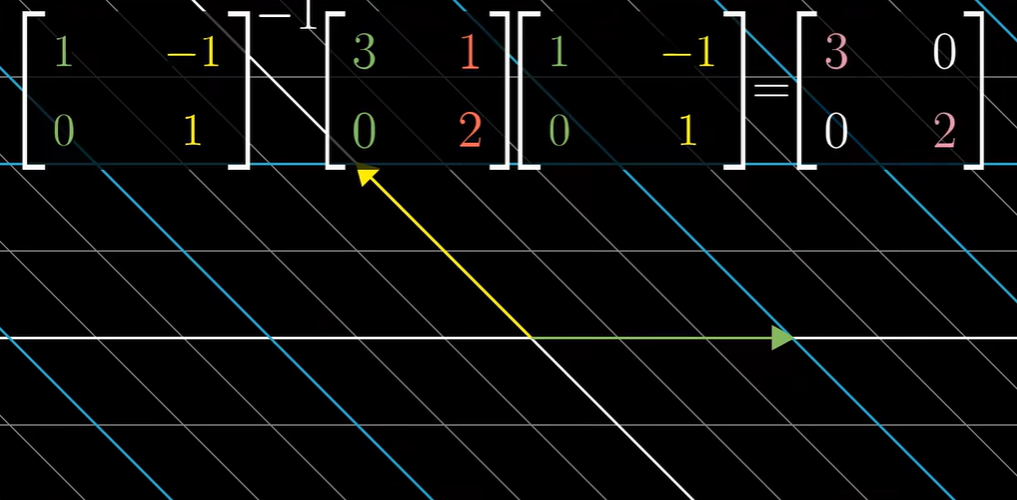 我们通过计算发现,在特征基的角度下看 A 只对坐标轴进行了伸拉操作,实现了对角化
从定义理解,A 对特征向量只起到了延长收缩作用,也就是说如果我们的坐标系是以它们为坐标轴,那么 A 对应的线性变换终究只是在坐标轴上的线性缩小和放大
所谓的对 A 的对角化操作,就是把式子变换一下,变成:
我们通过计算发现,在特征基的角度下看 A 只对坐标轴进行了伸拉操作,实现了对角化
从定义理解,A 对特征向量只起到了延长收缩作用,也就是说如果我们的坐标系是以它们为坐标轴,那么 A 对应的线性变换终究只是在坐标轴上的线性缩小和放大
所谓的对 A 的对角化操作,就是把式子变换一下,变成: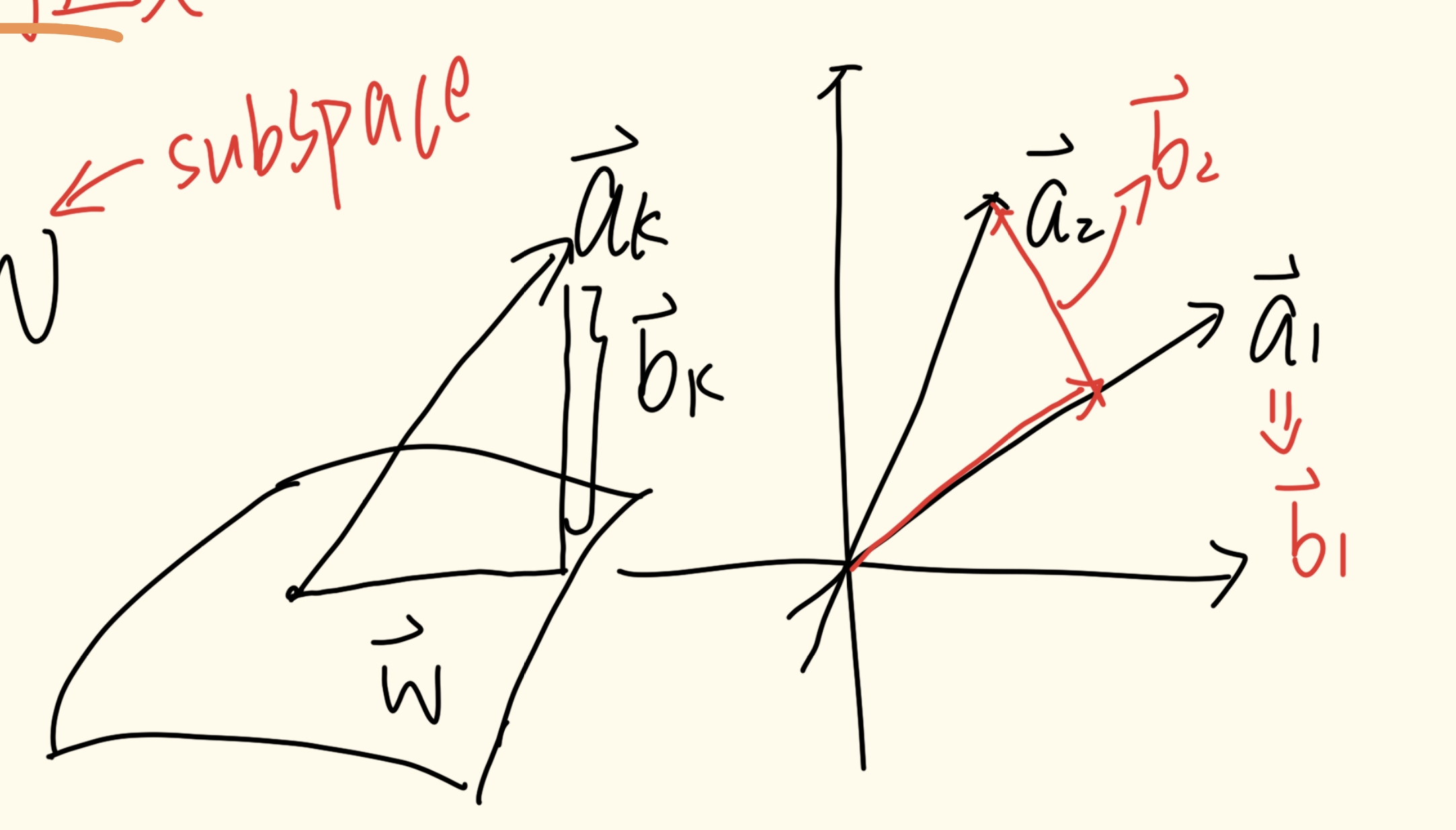 我们先令 ,
以此类推,第 i 个向量 等于第 i 个向量 减去 在前 i-1 个向量张成空间中的投影向量,这样不断循环最终可以得到一组正交基
这可以用一个循环程序的思想来叙述:
我们先令 ,
以此类推,第 i 个向量 等于第 i 个向量 减去 在前 i-1 个向量张成空间中的投影向量,这样不断循环最终可以得到一组正交基
这可以用一个循环程序的思想来叙述: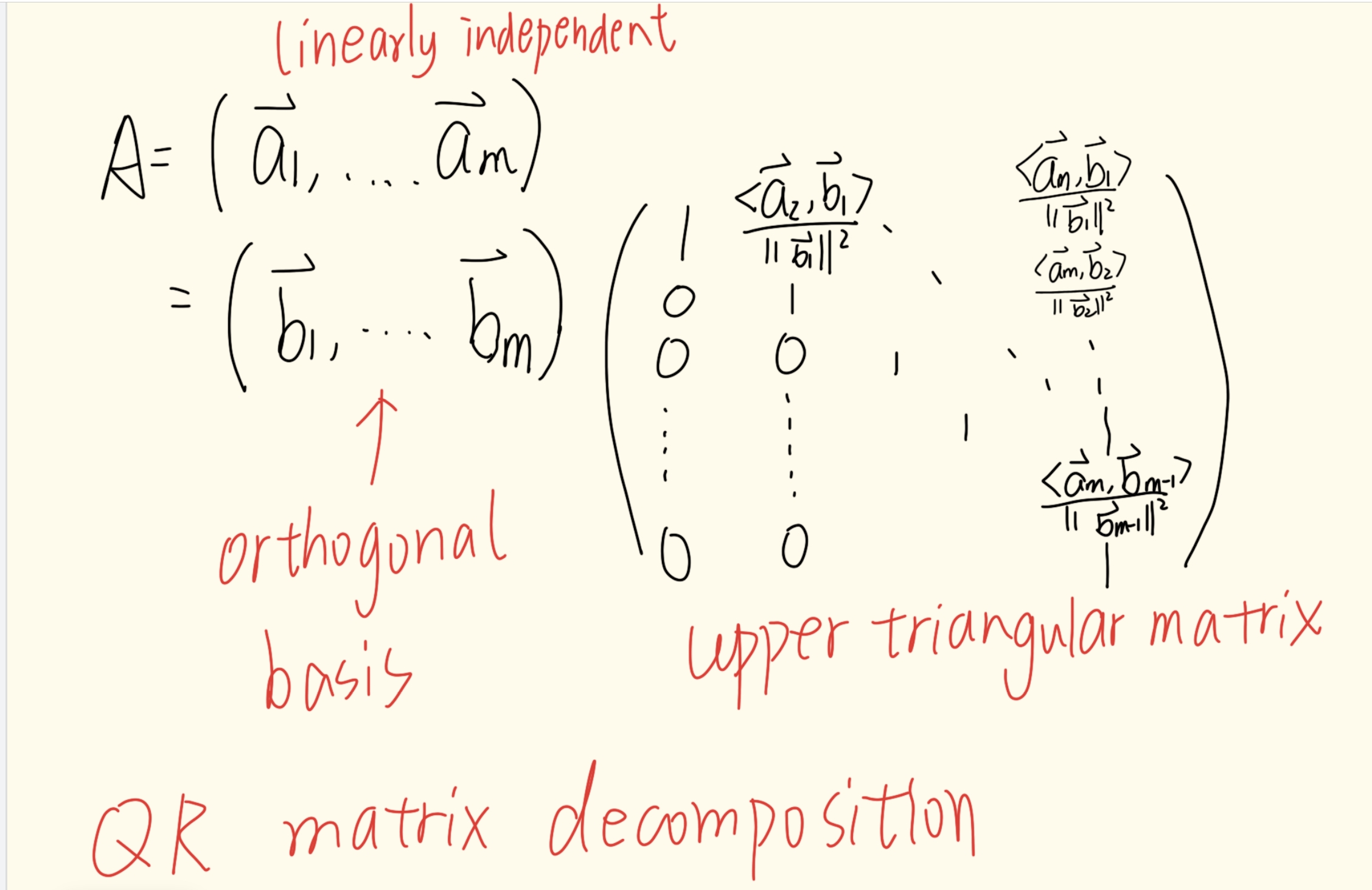 这个过程叫做 QR 分解
通常求 QR 分解的思路是先把所有的正交基求出来,再写出分解矩阵
这个过程叫做 QR 分解
通常求 QR 分解的思路是先把所有的正交基求出来,再写出分解矩阵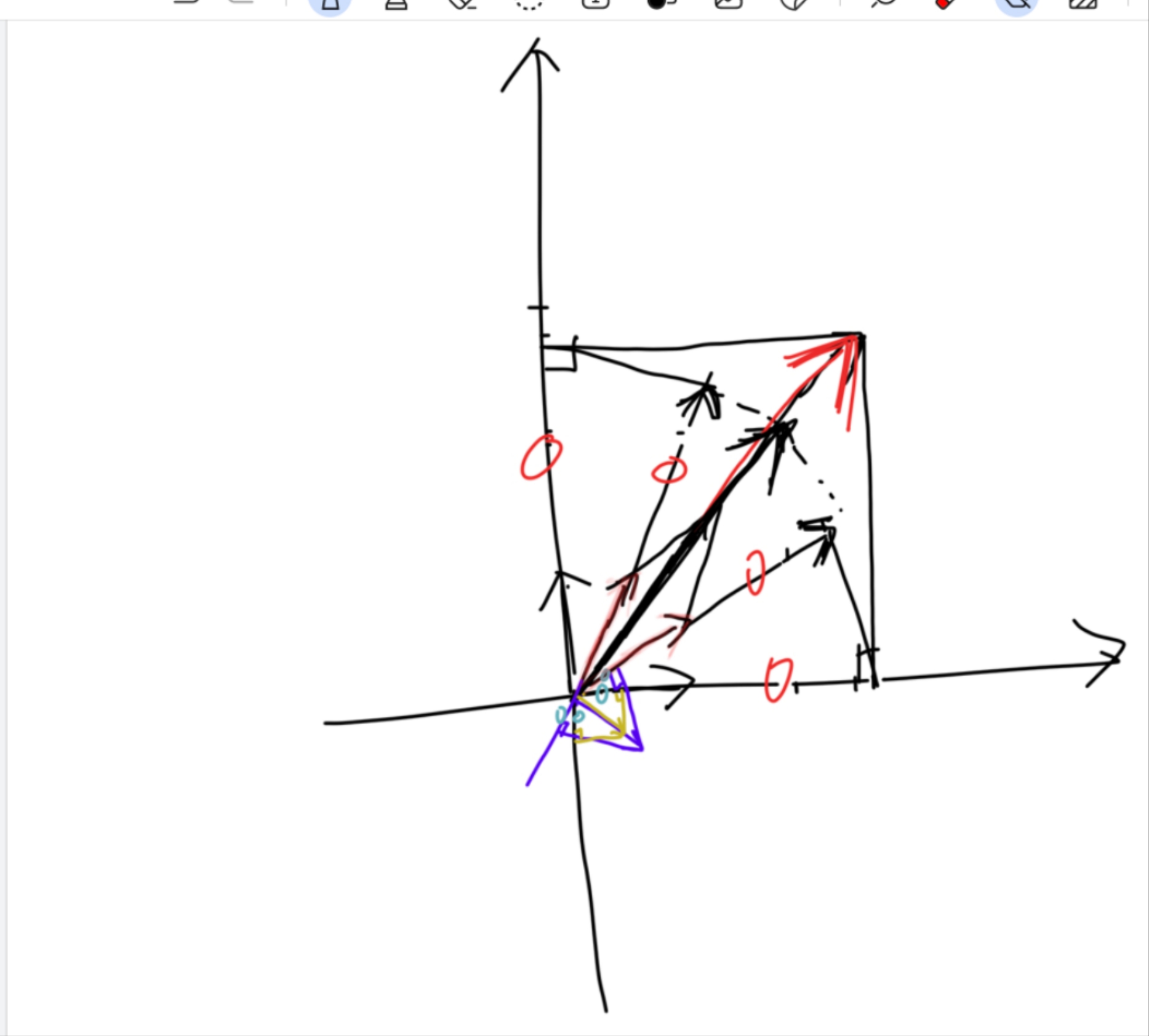 有的时候对于一些定理我们不一定要追求严格完整的理论证明(我们也不是抖 S 数学家对吧)。这一段证明其实需要通过数学归纳法进行一长串的推导,比较绕,所以我们可以通过一个特例画图分析来感性地理解这件事情
有的时候对于一些定理我们不一定要追求严格完整的理论证明(我们也不是抖 S 数学家对吧)。这一段证明其实需要通过数学归纳法进行一长串的推导,比较绕,所以我们可以通过一个特例画图分析来感性地理解这件事情